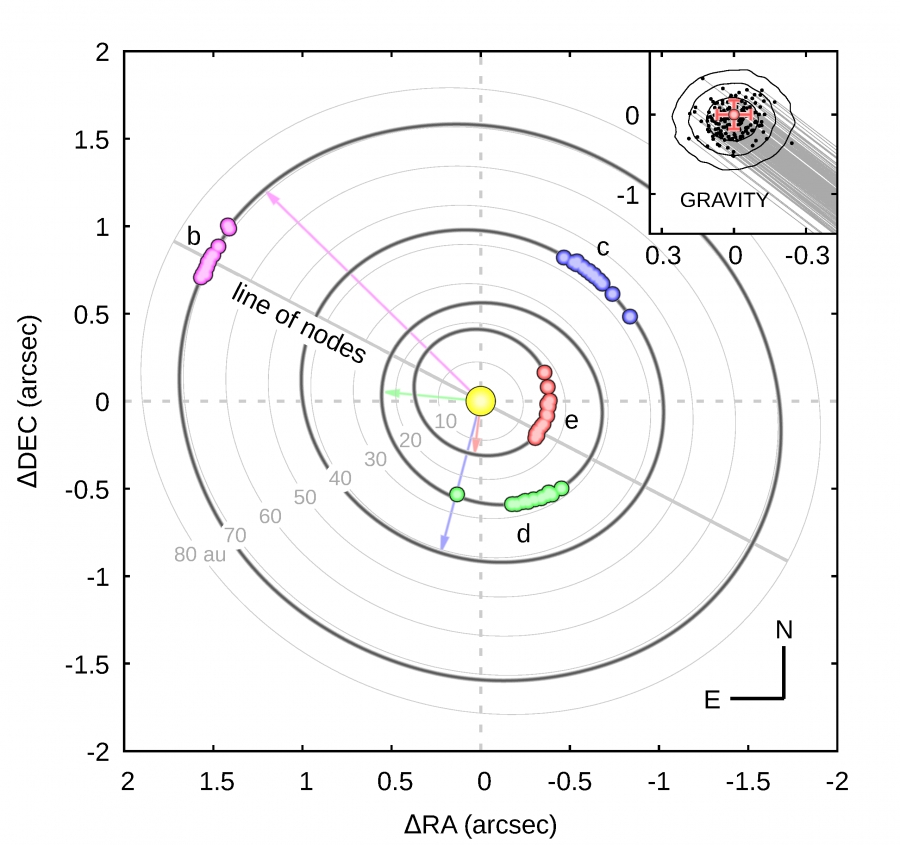
Prof. dr hab. Krzysztof Goździewski and dr hab. Cezary Migaszewski, prof. NCU published their latest results in the article "An Exact, Generalized Laplace Resonance in the HR 8799 Planetary System", Astrophysical Journal Letters, 2020, 902, id. L40. It is the result of many years of research, which allowed to find a stable and consistent with the observations orbital configuration of the system of four massive planets orbiting the star HR 8799.
The HR 8799 system is the first multi-planet extrasolar system discovered via direct imaging, which means that we actually observe the planets orbiting the star HR 8799. The situation is different in the case of indirect methods (e.g. radial velocities or transits), in which the existence of planets is inferred from the observation of the star, but not the planets themselves.
In 2008, three planets were discovered [1] at distances of 68, 38 and 24 astronomical units from the host star (these planets were marked with the letters b, c and d respectively), and two years later, the discovery of the fourth planet (marked with the letter e) was reported in distance of 15 astronomical units [2]. The masses of all planets were determined to be from a few to a dozen or so Jupiter masses.
This system almost immediately aroused great interest among astronomers studying extrasolar planets. The natural reason for this was that the HR 8799 is the first known system of this type. Equally important, however, were the difficulties associated with determining the orbital parameters of this system, and nothing attracts the attention of scientists as much as demanding problems.
The discovered planets are very distant from the star, so their orbital periods are very long. For the nearest planet e it is about 50 years, for the most distant planet b - about 450. The observational data, however, cover much shorter periods of time. Currently, it is about 10 years for planet e and about 20 years for the rest of the planets. Immediately after the discovery of the system, there was, naturally, even less. Even despite the high precision of the observations, the uncertainties in the determined orbital parameters were enormous.
The second problem was the large masses of the planets and the compactness of the system. The latter may be counter-intuitive, because we are talking about orbits, the sizes of which are measured in tens of astronomical units. What matter, however, are the ratios of these sizes, that is also the ratios of the orbital periods. The period of planet b equals approximately two periods of planet c, similarly the period of planet c is approximately twice the period of planet d, and finally the period of planet d equals approximately two periods of planet e. Considering all four planets, their orbital periods are close to the ratio 8:4:2:1. The commensurability of the orbital periods is called the mean motion resonance, and in the case when there are more than one pair of planets in resonance, we are talking about a chain of resonances. A well-known example of a configuration of this type in the solar system is the system of Jupiter's moons - Ganymede, Europa and Io, whose orbital periods are in the ratio 4:2:1.
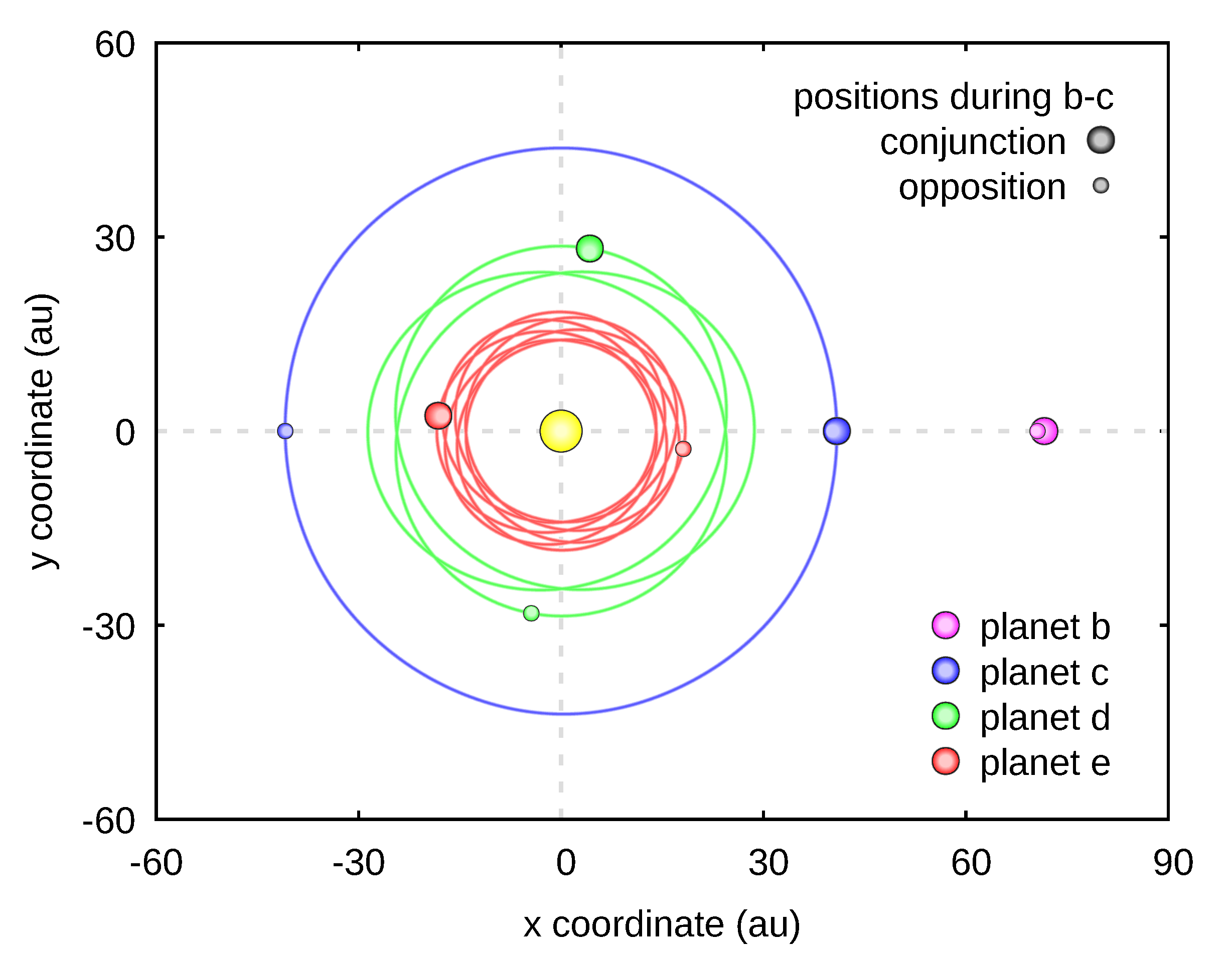
The planets in the multi-planet system disturb mutually their motions. If the planets are massive, these perturbations are strong. Additionally, in the case of commensurate orbital periods, perturbations may accumulate, and this may lead to destabilization of the system, i.e. to the ejection of one of the planets from the system, a planet-star collision or a collision between planets.
Shortly after the announcement of the discovery of the first three planets, it turned out that orbital configurations that fit the observations self-disrupt over hundreds of thousands of years [3]. Due to the relatively young age of the star, i.e. several tens of millions of years, the hypothesis that the system would actually disintegrate in the near future, which on an astronomical scale means tens of millions of years, was also initially considered [4]. However, it was largely an attempt to save the situation, as it would seem, with no way out. The problem of system stability became even more difficult after the discovery of the fourth planet.
Paradoxically, the solution to the problem turned out to be what was its source - the mean motion resonance. The commensurability of the orbital periods may, but not necessarily does lead to destabilization. The condition for stabilization, however, is appropriate synchronization of planetary motions. In other words, the system must be in exact resonance (otherwise called the periodic configuration) and not near resonance. In the case of massive planets, the proximity of resonance corresponds to unstable evolution, while only in a small range of parameters around the periodic configuration the planets motions are stable.
This area is extremely small, much smaller than the range of parameters allowed by the observations. The probability of finding a stable system among the possible configurations fitting the observations of the HR 8799 planets can be compared, somewhat playfully, to the probability of winning the lottery, and this in a situation where we do not play and we find the winning coupon by chance on the street. In fact, for several years after the discovery of the planets, no stable configurations could be found, although some of them could have had a lifetime of up to a billion years.
One way to find a stable configuration that fits the observations was to use the process of planetary migration being a result of planets interaction with a protoplanetary disc. Convergent migration, i.e. one in which the outer planet migrates towards the star faster than the inner planet, leads to mean motion resonances [5]. This fact was used to find resonant configurations, and then from a large set of such systems, those that correctly describe the observational data were selected [6]. This is basically a reverse of the classical method, in which you first look for systems that match the observations, and then select stable configurations from among them.
The approach described in article [6] proved successful, but could still be improved. One of the problems with the above method is that searching for resonant configurations as the final result of migration is computationally very demanding (calculations take a long time). More importantly, however, this method leads to an incomplete set of configurations, which in turn makes it difficult to determine the uncertainty of determining the orbital parameters.
Periodic configurations can also be found without reference to the migration process, since such systems evolve in a particular way. The system starting from a given point in the parameter space returns to this point after a certain finite time, called the period. Such configurations can be found in the process of numerical integration of the equations of motion as functions of planetary masses and the period ratio of a selected pair of planets. We say then that the periodic configurations form a hyper-surface in the parameter space with a dimension lower than the dimension of this space.
An example of a hyper-surface is a sphere (that is, a two-dimensional surface) immersed in three-dimensional space. If we knew otherwise that the systems we are interested in (more precisely: their representation in the parameter space) are located on the sphere, then there is no reason to search the entire three-dimensional space, and we can focus on this sphere. Although in the discussed issue concerning the HR 8799 system, the parameter space has many more dimensions than three, and the hyper-surface is very complicated, the principle of the method based on periodic configurations is exactly the same as in the example with a sphere.
The method using periodic configurations has been described in the article [7]. It allowed to determine the parameters of the HR 8799 system along with the uncertainties. It turned out, however, that the assumption of periodic configurations as acceptable types of systems binds the shapes of the orbits as well as the velocities of the planets in the orbits to such an extent that it was possible to correctly determine the distance to the system (i.e. about 129 light years) independently from the measurements of the heliocentric parallax. In general, this approach also allows the independent determination of the masses of the planets, but to do so requires additional, precise observations.
The system may contain hitherto unknown planets, both inside the orbit of planet e and outside the orbit of planet b. The search continues. It may be helpful to study discs consisting of small objects such as asteroids and planetoids. Their distribution in the system can be determined thanks to the infra-red emission of dust generated during the collisions between these objects [8]. On the other hand, an additional, as yet unobserved planet, acting by gravity, forms the structure of such discs [9]. The combination of the results of the above analyses may indicate potential areas in the system where such additional planets may exist.
Bibliography:
[1] Marois et al. 2008, Science, 322, 1348, doi:10.1126/science.1166585
[2] Marois et al. 2010, Nature, 468, 1080, doi:10.1038/nature09684
[3] Fabrycky and Murray-Clay, 2010, ApJ, 710, 1408, doi:10.1088/0004-637X/710/2/1408
[4] Goździewski and Migaszewski, 2009, MNRAS, 397, L16, doi:10.1111/j.1745-3933.2009.00674.x
[5] Snellgrove, Papaloizou and Nelson, 2001, A&A, 374, 1092, doi:10.1051/0004-6361:20010779
[6] Goździewski and Migaszewski, 2014, MNRAS, 440, 3140, doi:10.1093/mnras/stu455
[7] Goździewski and Migaszewski, 2020, ApJL, 902, L40, doi:10.3847/2041-8213/abb881
[8] Booth et al., 2016, MNRAS, 460, L10, doi:10.1093/mnrasl/slw040
[9] Goździewski and Migaszewski, 2018, ApJS, 238, id 6, doi:10.3847/1538-4365/aad3d3

 Piwnice k. Torunia, 87-148 Łysomice
Piwnice k. Torunia, 87-148 Łysomice