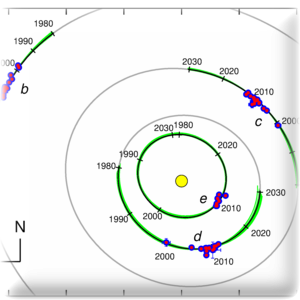
Three-decade long searches for extrasolar planets and growing number of detections (recently around 5000 objects – see: NASA web page) have contributed to the development of astronomy and astrophysics observational techniques as well as celestial mechanics and theory of dynamical systems. Current detection limits reach the Earth mass range (e.g., Kepler-186f) and even the Mars range (Kepler-138b). Rocky planets can exist in the habitable zones (appropriate for life) around their stars. Discovering of such objects is one of the aims of cosmic missions (like NASA projects Kepler and Kepler-K2, as well as the European astrometric survey GAIA with a precision of ~0.010 mas). Statistics of the Kepler detections shows that around 20% of Sun-like stars have an Earth-like planet in the habitable zone. Searching for extrasolar planets and the “second Earth” have not only a deep scientific, but also social and medial contexts, attracting wide public to astronomy and science in general.
There are numerous ground-based observational projects accompanying the cosmic missions searching for planets, e.g., projects based on the radial velocity technique with a precision below 1 m/s, that is sufficient for a few Earth mass planets detections (HARPS/HARPS-N ESO, HIRES Keck-I/II); photometric projects destined for transiting planets detections and transit timing (e.g., OGLE, HAT, WASP); astrometric projects based on the optic and radio interferometry (e.g., ALMA with a precision of ~0.1 mas at 1 mm wavelength, optical interferometers VLT, PRISM with a precision of 1 mas); direct imaging surveys (SPHERE VLT, AO Gemini, Subaru, Keck I/II, LBT, ROBO-AO) with the adaptive optics systems enabling detection levels of 0.1 mas.
Extrapolating current detection rate – currently, we know a few hundreds of two- and more planet systems – one may expect massive increase of the number of new detections. Observational projects generate huge amount of data available in the literature and public archives, the reduction of which is usually very complicated and time-consuming. One of the examples of that is the photometric observations of the Kepler satellite that indicate an existence of hundreds of systems with a few (up to 9) planets in each of them. Only small fraction of the systems were fully characterized. At the current, still fragmentary, level of understanding of this area of astrophysics, a comprehensive analysis of one planetary system is usually a subject of a refereed publication, and some of the systems, like HR8799 (Goździewski and Migaszewski 2014), were analysed and described in ~100 papers.
A statistical analysis of the observations (time series) enables preliminary characterisation of the orbital structure and physical parameters (like planets’ masses) together with reasonable parameters uncertainties. Nevertheless, the dynamical processes, stemming from the mutual gravitational, tidal and relativistic interactions between the star, the planets and the protoplanetary disc are what determines the evolutionary stability of such systems and characterize the constrains on their formation theories. The analysis of such processes, based on numerical simulations, refers to different time-scales and different dynamical effects that put constrains on the observed orbital architecture. One of the time-scales considered refers to the formation of a multi-planet system and the migration in a protoplanetary disc, i.e., first ~106-107 yr (e.g., Migaszewski 2015). Another time-scale is related to the short-period evolution (tens to hundreds of the orbital periods), determined by the low-order mean motion resonances, which can be measured with a help of the transits timing (Migaszewski et al. 2012, Goździewski et al. 2016, Migaszewski et al. 2016, Panichi et al. 2016). The intermediate secular time-scale (103-106 yr) contains both the planet-planet interactions, as well as conservative effects resulting from the non-spherical shape of the star and the planets, which are treated as extended objects. When studying the whole (evolutionary) time-scale of the system, i.e., ~108-109 yr, one needs to account for dissipative effects (tides and energy dissipation in the star and the planets, mass loss of the star).
Modelling the observations of stars with planets
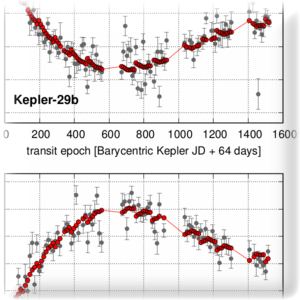The aim of this topic is to observationally determine the initial orbital elements and masses of planetary systems, in particular those involved in mean motion resonances (commensurability of the orbital periods), which result in very complicated structure of the phase space and long-term dynamics. The analysis refers to radial velocities (Goździewski et al. 2013), astrometric observations (Gawroński et al. 2016), transits (Goździewski et al. 2016, Migaszewski et al. 2016), transit timing (Goździewski et al. 2012, 2015) and direct imaging (Goździewski and Migaszewski 2014). Moreover, indirect effects relying on variation of the observational signal resulting from the mutual gravitational interactions might be used as observables (e.g., Transit Timing Variation or Light Travel Time). A degree of the observational models complication increases with the number of planets (free parameters of the model) and can reach values of order 100 for a system of ten planets, which is comparable with the number of planets in the Solar system. In most of the cases, the observations of particular systems need to be considered individually, accounting for the type of observations, the observational instruments used, data sampling and quality, as well as the character of the analysed system (resonant, hierarchical, a planet in a binary star system).
The limited set of observations is a basic problem in the analysis. Typically, only one or two components of the barycentric position or velocity of the star are available or the data are indirect (e.g., the changes in the transit times). One-dimensional observations (like the radial velocities) introduce the degeneracy into the model, e.g., it is difficult to constrain the inclinations of the orbits or the planets’ masses without using the time-consuming N-body model of motion.
Orbital stability analysis in different time-scales
The analysis refers to both the planetary systems with one central star and with more stars. One of the problems in this case results from the differences in characteristic time-scales, which is caused by wide ranges of the semi-major axes or complex dynamical environments (e.g., hierarchical, near-resonant or Trojan type configurations). The short-term stability analysis makes it possible to put constrains on the parameters that cannot be well-determined from observations alone. Moreover, that allows to predict areas in the parameter space, corresponding to potential components of the system, the signals of which being below the detection level (Goździewski and Migaszewski 2014). From the computational point of view, it is important to develop efficient methods of deterministic chaos detection (e.g., Panichi et al. 2016) in order to eliminate initial conditions resulting in unstable orbital evolution. In order to study the structure of the phase space one needs MPI codes for the dynamical maps, like Mechanic (Słonina et al. 2015) and currently we are developing our new code of this sort μFarm (Goździewski, in preparation). The codes can be run both on CPU clusters as well as on GPU graphic cards.
Secular and resonant evolution of planetary systems
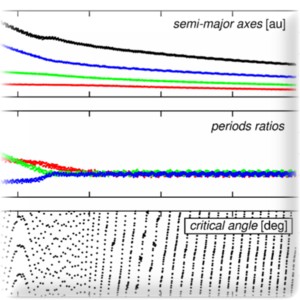In order to describe the orbital evolution of a planetary system during its lifetime, one needs to account for various types of time-dependent perturbations to the point-mass gravitation (e.g., rotational distortion of the star, tidal deformation of the star and the planet, relativistic corrections, Migaszewski 2012).
Currently, we are focusing on the planetary migration that results in catching the planets into mean motion resonances at early stages of the system evolution (Migaszewski et al. 2013, Migaszewski 2015). Those effects have to be considered not only when studying the evolution, but also as a component of the goal function for some of the observational models (Goździewski and Migaszewski 2014, Goździewski et al. 2016, Migaszewski et al. 2016).
Systems involved in mean motion resonances are a particularly interesting and basic goal of our studies. The resonances are formed at early stages of the systems formation and constitute sort of fossils of the formation processes and early orbital evolution.
Asteroid and dust discs are another objects that have resonant structure, which is determined by the massive planets and their long-term orbital dynamics (migration).
Numerical simulations make it possible to understand the planetary systems dynamics, which helps us to constrain the allowed ranges of the physical parameters (planets’ masses) and initial conditions and point particular configurations (equilibria, periodic orbits), which determine the structure of the phase space (Goździewski et al. 2013, Goździewski and Migaszewski 2014, Goździewski et al. 2016, Migaszewski et al. 2016).
Group members:
- prof. Krzysztof Goździewski
- dr Cezary Migaszewski
Most important publications:
- Panichi F., Goździewski K., Turchetti G. (2017) The reversibility error method (REM): a new, dynamical fast indicator for planetary dynamics, MNRAS 468, 469
- Gawroński M., Goździewski K., Katarzyński K. (2017) Physical properties and astrometry of radio-emitting brown dwarf TVLM 513-46546 revisited, MNRAS 466, 4211
- Migaszewski C., Gozdziewski K., Panichi F. (2016) The origin and 9:7 MMR dynamics of the Kepler-29 system, MNRAS 465, 2366
- Goździewski K., Migaszewski C., Panichi F., Szuszkiewicz E. (2016) The Laplace resonance in the Kepler-60 planetary system, MNRAS 455, L104
- Migaszewski C. (2015) On the migration of two planets in a disc and the formation of mean motion resonances, MNRAS 453, 1632
- Goździewski K., Słowikowska A., Dimitrov D. et al. (including Gawroński M., Nowak G., Kubicki D.) (2015) The HU Aqr planetary system hypothesis revisited, MNRAS 448, 1118
- Słonina M., Goździewski K., Migaszewski C. (2015) Mechanic: the MPI/HDF framework for the dynamical astronomy, New Astronomy 34, 98
- Goździewski K., Migaszewski C. (2014) Multiple mean motion resonances in the HR 8799 planetary system, MNRAS 440, 3140
- Migaszewski C., Goździewski K., Słonina M. (2013) A linear distribution of orbits in compact planetary systems?, MNRAS 436, L25
- Goździewski K., Słonina M., Migaszewski C., Rozenkiewicz A. (2013) Testing a hypothesis of the ν Octantis planetary system, MNRAS 430, 533
- Migaszewski C., Słonina M., Goździewski K. (2012) A dynamical analysis of the Kepler-11 planetary system, MNRAS 427, 770
- Goździewski K., Nasiroglu I., Słowikowska A. et al. (2012) On the HU Aquarii planetary system hypothesis, MNRAS 425, 930
- Migaszewski C. (2012) The generalized non-conservative model of a 1-planet system revisited, Celestial Mechanics and Dynamical Astronomy 113, 169
- Migaszewski C., Goździewski K. (2009) Secular dynamics of a coplanar, non-resonant planetary system under the general relativity and quadrupole moment perturbations, MNRAS 392, 2
- Goździewski K., Bois E., Maciejewski A.J., Kiseleva-Eggleton L. (2001) Global dynamics of planetary systems with the MEGNO criterion, A&A 378, 569