Dynamika układów planetarnych

Trwające trzecią dekadę poszukiwania planet pozasłonecznych i rosnąca lawinowo liczba detekcji (obecnie ponad 5000 obiektów – aktualne dane w witrynie NASA) . przyczyniły się nie tylko do rozwoju astronomii i astrofizyki w dziedzinie technik obserwacyjnych, astrofizyki ale także mechaniki nieba i teori układów dynamicznych. Obecne progi detekcji osiągają poziom mas tzw. super-Ziemi, rzędu masy Neptuna, a nawet porównywalnych z Ziemią (np. Kepler-186f) i mniejszych, o masie Marsa (Kepler-138b). Planety skaliste mogą istnieć w obszarach tzw. strefy „zamieszkiwalnej”, sprzyjającej rozwojowi życia. Odkrycie takich globów było i jest celem misji kosmicznych (np. projekty NASA Kepler i Kepler-K2 oraz aktualny europejski przegląd astrometryczny GAIA z precyzją ∼ 0.010 mas). Statystyka detekcji planet przez teleskop Kepler dowodzi, że ok. 20% gwiazd typu słonecznego ma planetę porównywalną z Ziemią w strefie zamieszkiwalnej. Poszukiwania planet pozasłonecznych i „drugiej Ziemi” mają nie tylko bogaty kontekst naukowy, ale także społeczny i medialny, przyciągając szeroką publiczność do astronomii i nauk ścisłych.
Misjom kosmicznym poszukującym planet towarzyszą liczne obserwacyjne projekty naziemne, np.: metodą prędkości radialnych z precyzją poniżej 1 m/s, która wystarcza do detekcji planet rzędu kilku mas Ziemi (HARPS/HARPS-N ESO, HIRES Keck-I/II); projekty fotometryczne, ukierunkowane na wykrywanie planet tranzytujących i chronometraż zaćmień (np. OGLE, HAT, WASP i inne przeglądy naziemne); projekty astrometryczne, oparte o interferometrię optyczną i radiową (np. ALMA w dziedzinie radiowej na falach 1 mm zapewnia precyzję astrometryczną ∼ 0.1 mas, interferometry optyczne (np. VLT, PRISM) zapewniające astrometrię poniżej 1 mas); przeglądy metodą bezpośredniego obrazowania (SPHERE VLT, systemy AO Gemini, Subaru, Keck I/II, LBT, ROBO-AO) z systemami optyki adaptacyjnej zapewniają progi detekcji astrometrycznej na poziomie 0.1 mas.
Ekstrapolując dotychczasowe tempo odkryć systemów pozasłonecznych — obecnie znamy kilkaset takich systemów z więcej niż jedną planetą — można się spodziewać lawinowego przyrostu nowych detekcji. Projekty obserwacyjne generują bardzo duże ilości danych dostępnych w literaturze i publicznych archiwach danych, których redukcja i interpretacja jest zwykle skomplikowana i czasochłonna. Jako przykład można podać obserwacje fotometryczne sondy Kepler, które już obecnie zawierają wskazanie na setki układów wielokrotnych, zawierających od 2,3 do 8–9 planet. Tylko niewielka część z nich została w pełni scharakteryzowana. Na obecnym, wciąż fragmentarycznym poziomie zrozumienia tej części astrofizyki, wyczerpująca analiza jednego układu planetarnego jest zazwyczaj przedmiotem recenzowanej publikacji, a niektóre systemy planarne, jak HR 8799 (Goździewski and Migaszewski, 2014) doczekały się ∼ 100 artykułów.
Analiza statystyczna obserwacji (szeregów czasowych) pozwala na wstępne określenie budowy orbitalnej i cech fizycznych (np. mas planet) oraz realistycznych niepewności parametrów orbitalnych i fizycznych. Jednak to procesy dynamiczne zachodzące w różnych skalach czasowych, będące wynikiem wzajemnych oddziaływań grawitacyjnych, pływowych i relatywistycznych pomiędzy gwiazdą, planetami oraz dyskiem protoplanetarnym, determinują ewolucyjną stabilność takich systemów oraz określają więzy teorii ich formowania. Ich analiza oparta na symulacjach numerycznych dotyczy różnych skal czasowych jak i efektów dynamicznych, które nakładają więzy na obserwowaną architekturę orbitalną. Skale te obejmują formowanie się układu wielokrotnego i migrację w dysku protoplanetarnym ∼ 10⁶ –10⁷ lat, np. (Migaszewski, 2015); ewolucję krótkookresową, determinowaną przez rezonanse ruchów średnich niskich rzędów, która może być mierzalna np. przez chronometraż zaćmień i tranzytów ∼ 10⁷ lat (Migaszewski et al., 2012; Goździewski et al., 2016; Migaszewski et al., 2016; Panichi et al., 2016). W pośredniej skali wiekowej uwzględniamy zarówno oddziaływania planetarne, jak i zachowawcze (konserwatywne) efekty zaburzeń potencjału grawitacyjnego mas punktowych przybliżających gwiazdę i planety. Determinują one długookresową stabilność w skali 10⁸ lat. Wreszcie istotna jest pełna skala ewolucyjna, której model dynamiczny musi uwzględniać efekty dyssypatywne (pływów i rozpraszania energii, utraty masy przez gwiazdę) w skali 10⁸ –10⁹ lat, zależnie od interwału cyklu ewolucyjnego gwiazdy macierzystej lub macierzystego układu gwiazdowego w przypadku gwiazd podwójnych.

Modelowanie obserwacji gwiazd z układami planetarnymi

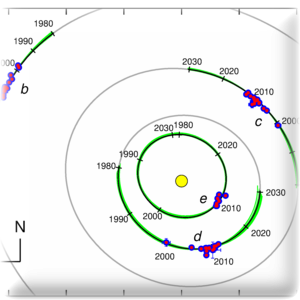
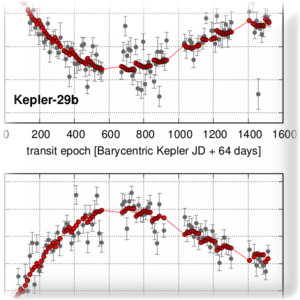Temat ten ma na celu możliwie pełne, obserwacyjne wyznaczenie warunków początkowych (opisu orbit) układów planetarnych, w szczególności związanych rezonansami orbitalnymi (współmiernościami okresów orbitalnych), które implikują bardzo skomplikowaną strukturę przestrzeni fazowej i długookresowej dynamiki. Analiza obejmuje obserwacje metodą prędkości radialnych (Goździewski et al., 2013), uzyskanymi metodą astrometryczną (Gawroński et al., 2016), metodą tranzytów (Goździewski et al., 2016; Migaszewski et al., 2016), chronometrażu zaćmień (Goździewski et al., 2012, 2015) oraz bezpośredniego obrazowania (Goździewski and Migaszewski, 2014). Mogą być wykorzystane efekty pośrednie oparte o zmianę obserwowanego sygnału na skutek wzajemnych oddziaływań grawitacyjnych (np. tzw. Transit Timing Variation lub Light Travel Time). Stopień komplikacji modeli obserwacyjnych rośnie z ilością planet (wolnych parametrów modelu obserwacyjnego) i może osiągnąć wartości rzędu 100 dla systemu dziesięciu planet, porównywalnego liczebnością składników do Układu Słonecznego. W większości przypadków obserwacje konkretnych systemów planetarnych należy rozpatrywać praktycznie indywidualnie, biorąc pod uwagę rodzaj obserwacji, użyte instrumenty, próbkowanie i jakość pomiarów, ale także charakter analizowanego systemu (rezonansowy, hierarchiczny, w gwiazdowym układzie podwójnym).
Podstawowym problemem jest dostępność ograniczonego zbioru obserwacji. Zwykle bowiem dysponujemy tylko jedną lub dwiema składowymi położenia lub prędkości gwiazdy względem barycentrum lub danymi pośrednimi (np. zmianami momentów zaćmień). Obserwacje jednowymiarowe (jak prędkość radialna) wprowadzają przez to degeneracje, np. trudno jest na ich podstawie wyznaczyć nachylenie orbit lub masy planet bez użycia czasochłonnego modelowania oddziaływań N-body pomiędzy wszystkimi składnikami danego systemu.

Analiza stabilności orbitalnej w różnych skalach czasowych

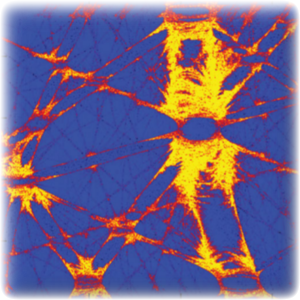Zagadnienie to dotyczy zarówno układów z jedną gwiazdą centralną jak również wielokrotnych systemów gwiazdowych. Problemem w tym przypadku są różnice skal czasowych spowodowane dużymi zakresami półosi orbitalnych lub skomplikowanymi środowiskami dynamicznymi, takimi jak np. układy hierarchiczne lub blisko-rezonansowe, systemy z planetami trojańskimi. Analiza stabilności krótkookresowej pozwala wprowadzić więzy na te parametry badanych układów, które nie mogą być dobrze określone obserwacyjnie. Pozwala to przewidywać obszary w przestrzeni warunków początkowych, odpowiadające potencjalnym składnikom układu, których sygnały byłyby poniżej progu detekcji (Goździewski and Migaszewski, 2014). Z obliczeniowego punktu widzenia istotne jest dla tego typu podejścia opracowanie efektywnych metod detekcji chaosu deterministycznego (np. Panichi et al., 2016) dla eliminowania warunków początkowych skutkujących niestabilną ewolucją orbitalną.
Dla analizy struktury przestrzeni fazowej potrzebujemy kody MPI dla map dynamicznych, jak Mechanic (Słonina et al., 2015) i aktualnie rozwijany nasz nowy kod farmy obliczeniowej μFarm (Goździewski, w przygotowaniu). Są one uruchamiane na klasterach CPU, jak i kartach graficznych GPU.

Ewolucja wiekowa i rezonansowa systemów planetarnych

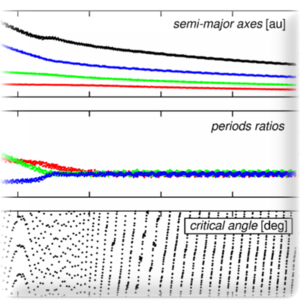Aby opisać ewolucję orbitalną układu planetarnego w skali życia gwiazdy należy uwzględnić zmienne w czasie zaburzenia punktowego potencjału grawitacyjnego Newtona o różnym charakterze (np. dystorsji rotacyjnej gwiazdy wynikającej z jej wieku, odkształceń pływowych figur gwiazdy i planet, spowodowanych oddziaływaniem bryła–bryła, poprawek relatywistycznych (Migaszewski, 2012).
Obecnie najwięcej uwagi poświęcamy zjawisku migracji planetarnej, które prowadzi do wychwytu planet w rezonanse orbitalne we wczesnych etapach ewolucji (Migaszewski et al., 2013; Migaszewski, 2015). Efekty te często należy uwzględnić nie tylko ewolucji układu, ale także jako komponent funkcji celu dla niektórych modeli obserwacyjnych (Goździewski and Migaszewski, 2014; Goździewski et al., 2016; Migaszewski et al., 2016).
Szczególnie interesującym i podstawowym celem naszych badań są układy planet w rezonansach orbitalnych. Takie rezonanse powstają we wczesnych fazach ewolucji układów wielokrotnych i stanowią swego rodzaju skamieliny procesów formowania oraz wczesnej ewolucji orbitalnej. Rezonansowy charakter mają również dyski asteroidalne i pyłowe, których strukturę determinują z kolei orbity masywnych planet, oraz długookresowa ewolucja orbitalna (migracja). Zrozumienie tej struktury jest możliwe tylko dzięki symulacjom numerycznym, dzięki którym możemy określić dopuszczalne zakresy parametrów fizycznych (mas) i warunków początkowych oraz wskazać rozwiązania szczególne (położeń równowagi, orbit okresowych), które determinują strukturę przestrzeni fazowej (Goździewski et al., 2013; Goździewski and Migaszewski, 2014; Goździewski et al., 2016; Migaszewski et al., 2016).

Grupa:

• prof. Krzysztof Goździewski
• dr Cezary Migaszewski

Najważniejsze prace:

• Panichi F., Goździewski K., Turchetti G. (2017) The reversibility error method (REM): a new, dynamical fast indicator for planetary dynamics, MNRAS 468, 469
• Gawroński M., Goździewski K., Katarzyński K. (2017) Physical properties and astrometry of radio-emitting brown dwarf TVLM 513-46546 revisited, MNRAS 466, 4211
• Migaszewski C., Gozdziewski K., Panichi F. (2016) The origin and 9:7 MMR dynamics of the Kepler-29 system, MNRAS 465, 2366
• Goździewski K., Migaszewski C., Panichi F., Szuszkiewicz E. (2016) The Laplace resonance in the Kepler-60 planetary system, MNRAS 455, L104
• Migaszewski C. (2015) On the migration of two planets in a disc and the formation of mean motion resonances, MNRAS 453, 1632
• Goździewski K., Słowikowska A., Dimitrov D. i in. (w tym z IA UMK: Gawroński M., Nowak G., Kubicki D.) (2015) The HU Aqr planetary system hypothesis revisited, MNRAS 448, 1118
• Słonina M., Goździewski K., Migaszewski C. (2015) Mechanic: the MPI/HDF framework for the dynamical astronomy, New Astronomy 34, 98
• Goździewski K., Migaszewski C. (2014) Multiple mean motion resonances in the HR 8799 planetary system, MNRAS 440, 3140
• Migaszewski C., Goździewski K., Słonina M. (2013) A linear distribution of orbits in compact planetary systems?, MNRAS 436, L25
• Goździewski K., Słonina M., Migaszewski C., Rozenkiewicz A. (2013) Testing a hypothesis of the ν Octantis planetary system, MNRAS 430, 533
• Migaszewski C., Słonina M., Goździewski K. (2012) A dynamical analysis of the Kepler-11 planetary system, MNRAS 427, 770
• Goździewski K., Nasiroglu I., Słowikowska A. i in. (2012) On the HU Aquarii planetary system hypothesis, MNRAS 425, 930
• Migaszewski C. (2012) The generalized non-conservative model of a 1-planet system revisited, Celestial Mechanics and Dynamical Astronomy 113, 169
• Migaszewski C., Goździewski K. (2009) Secular dynamics of a coplanar, non-resonant planetary system under the general relativity and quadrupole moment perturbations, MNRAS 392, 2
• Goździewski K., Bois E., Maciejewski A.J., Kiseleva-Eggleton L. (2001) Global dynamics of planetary systems with the MEGNO criterion, A&A 378, 569