Projekty numeryczne
PIERNIK MHD
Piernik jest kodem magnetohydrodynamicznym stworzonym i rozwijanym w Instytucie Astronomii Uniwersytetu Mikołaja Kopernika w Toruniu. Aktualna wersja kodu wykorzystuje prosty, zachowawczy schemat numeryczny, t.j. Relaxing TVD (RTVD). Ogólny matematyczny opis relaksacji zachowawczych, hiperbolicznych układów równań różniczkowych cząstkowych i związane z nimi metody numeryczne, został przedstawiony przez Jin i Xin (1995). Konkretna implementacja algorytmu RTVD, która jest wykorzystywana w Pierniku została opracowana przez Trac & Pen (2003) i Pen et al. (2003), gdzie metodę przedstawiono w przystępny sposób, a także dołączono krótkie, open source wersje kodów HD i MHD. Kody te opierają się na kierunkowym podziale (ang. directional split) i implementuja schemat drugiego rzędu zarówno w czasie jak i przestrzeni. RTVD jest łatwo rozszerzalny do obliczeń z wykorzystaniem dodatkowych składników: neutralnego lub zjonizowanego gazu, pyłu, promieniowania kosmicznego; oraz dodatkowych procesów fizycznych, takich jak oddziaływania międzypłynowe i oporność magnetyczna ośrodka, samograwitacja. Prostota i mała liczba operacji zmiennoprzecinkowych podstawowego algorytmu znajduje odzwierciedlenie w wydajności zono-cykli / s (na jeden rdzeń ∼ 2 GHz).
Uczestnicy projektu (IA UMK): prof. dr hab. Michał Hanasz, dr Dominik Wóltański, dr Nicolas Peschken, mgr Mateusz Ogrodnik
Pozostali wpsółautorzy (spoza IA UMK): dr Kacper Kowalik (NCSA, Illinois), dr Artur Gawryszczak (CAMK PAN Warszawa), dr Varadarajan Parthasarathy (HLRS Stuttgart)
Strona projektu
Repozytorium kodu
MECHANIC
Mechanic jest zaawansowanym środowiskiem numerycznym, którego głównym zadaniem jest pomoc w prowadzeniu długotrwałych symulacji numerycznych na klastrach obliczeniowych. Kod oparty jest o technologię MPI (Message Passing Interface), a komunikacja międzyprocesorowa odbywa się w ramach tzw. farmy. Struktura kodu pozwala na całkowitą separację warstwy konfiguracji, komunikacji i zapisu danych (tzw. rdzeń) od właściwego zagadnienia numerycznego (moduł numeryczny). Oprogramowanie dostarcza bogate API (Application Programming Interface), dzięki któremu użytkownik może łatwo zaimplementować problemy numeryczne. W odróżnieniu od istniejących kodów z rodziny tzw. task management systems (np. Condor, Workqueue), Mechanic stara się ujednolicić warstwę komunikacji, konfiguracji i zapisu danych.
Kod napisany jest w języku C i dostępny na licencji BSD.
Do głównych zalet kodu należą:
- Sepracja warstwy konfiguracji i komunikacji oraz zapisu danych
- Przejrzyste API
- Automatyczne tworzenie kopii zapasowych w trakcie symulacji
- Nie blokująca komunikacja międzyprocesorowa
- Zapis danych w otwartym formacie HDF5
Zaangażowane osoby: prof. dr hab. Krzysztof Goździewski, mgr Mariusz Słonina, dr Cezary Migaszewski
Strona projektu
Repozytorium kodu
INHOMOG
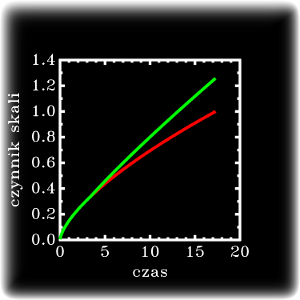
Biblioteka programistyczna “libinhomog” służy do obliczeń średniej ekspansji kosmologicznej. Zawiera ona przykładowy program “inhomog”, demonstrujący ewolucję efektywnego czynnika skali we wszechświecie, którego przekrój przestrzenny ma topologię 3-torusa i jest podzielony na domeny, w których wykonywane jest uśrednianie. Biblioteka umożliwia całkowanie równań Landau-Raychaudhuri ewolucji średniego czynnika skali, wykorzystując analityczne formuły kinematycznej reakcji wstecznej Q_D. Biblioteka udostępnia procedurę wywoływaną przez oprogramowanie RAMSES, zmodyfikowane dostarczoną łatą programistyczną “ramses-scalav”. Możliwe jest wykorzystanie programu “inhomog” z poziomu linii poleceń w celu analizy roli wirializacji jako potencjalnej alternatywy dla ciemnej energii (zob. Roukema 2017, arXiv:1706.06179). Ten opis, jak również sam kod jest dostarczony na licencji GNU GPL.
Zaangażowane osoby: dr hab. Boudewijn Roukema, prof. UMK, dr Jan Ostrowski
RAMSES-SCALAV
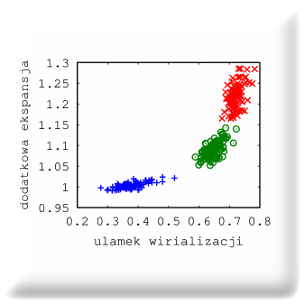
Pakiet ramses-scalav jest rozszerzeniem oprogramowania RAMSES, który wykorzystywany jest jako front-end dla bibliotek DTFE i inhomog w celu symulacji ewolucji kosmologicznych warunków początkowych (wygenerowanych np. przez oprogramowanie mpgrafic). Pakiet oblicza efektywną (globalną) ewolucję czynnika skali jako uśrednioną objętościowo ewolucję czynnika skali a_D zależnego od domeny, w oparciu o całkowanie równania Landau-Raychaudhuri. W ujęciu relatywistycznym takie podejście powinno być bardziej realistyczne aniżeli założenie ewolucji czynnika skali w oparciu o model Friedmann-Lemaitre-Robertson-Walker’a. Opis ten, jak również sam kod jest dostarczony na licencji Cecill. Szczegóły i uzasadnienia naukowe są dostępne w artykule Roukema (2017, arXiv:1706:06179).
Zaangażowane osoby: dr hab. Boudewijn Roukema, prof. UMK, dr Jan Ostrowski